For my Computability final paper, I wrote about the Church-Rosser Theorem and the consistency of λ-calculus, as well as introducing the general theory of λ-calculus and showing how arithmetic can be performed within it.

What is the Church-Rosser Theorem?

The main operation of λ-calculus (at least in its standard form) is β-reduction. Loosely speaking, β-reduction means that, given a function that takes an argument \(x\) and returns \(M\), applying this function to some argument \(y\) yields the same result as substituting \(y\) for every occurrence of \(x\) in \(M\). In the notation of λ-calculus, we write this as:

where \((λx.M)\) means “the function that returns \(M\) given \(x\)” and \(M[x := y]\) means “the result of substituting \(y\) for \(x\) in \(M\)”.

A statement \(M\) can be β-reduced to \(N\) if you can apply the above formula some number of times to \(M\) to turn it into \(N\).

For example, \(((λx.(λy.y))z)z\) β-reduces to \(z\), because

The Church-Rosser Theorem for β-reduction states that whenever some expression \(M\) can be β-reduced to two different expressions \(N\) and \(P\), there exists some expression \(Q\) that both \(N\) and \(P\) can β-reduce to. This property is also called confluence, and is sometimes referred to as the diamond property, because the resulting graph of reductions looks like this:

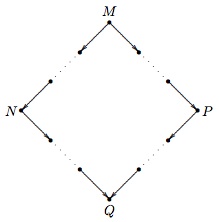
Proving the Church-Rosser Theorem

In my paper, my proof of the Church-Rosser mainly follows the classic Tait-Martin-Löf proof, which is well-known as one of the simplest proofs of the theorem, relying on nothing more than a basic understanding of the theory of β-reductions.

The proof has three stages:

• First, I introduce a new notion of reduction, that I call ◊, and show that ◊ satisfies the diamond property. In this section, I follow Barendregt’s exposition of the Tait-Martin-Löf proof.
• Next, I show that ◊-equivalence is the transitive closure of β-equivalence. In other words, the β-equivalence relation is the minimal superset of the ◊-equivalence relation that satisfies transitivity.
• Finally, I prove the Strip Lemma, which states that if a notion of reduction satisfies the diamond property, then so does its transitive closure. Thus, since ◊ satisfies the diamond property, so does β. I primarily follow Robert Pollack’s simplified proof of the Strip Lemma.

What does this mean for consistency?

In the final section of my paper, I show that it follows from the Church-Rosser Theorem that every expression in λ has a unique “β-normal form” - that is, a unique form from which the expression cannot be β-reduced any further.

Then, I show that two terms cannot be equal to each other in λ-calculus if they are not β-equivalent. This is a result that follows directly from the axioms of λ-calculus.

Putting all of these pieces together, if two terms \(M\) and \(N\) do not share the same β-normal form, then the statement \(M = N\) is not provable in λ-calculus.

It’s easy to find two terms that do not share a β-normal form - for example, \(I = λx.x\) and \(K = λx.(λy.x)\). Thus, the statement \(I = K\) is not provable in λ-calculus, and so λ-calculus is a consistent theory, because if λ-calculus were inconsistent, then by definition every (syntactically valid) statement would be provable in it.

Interested in this sort of thing?

If this has piqued your interest, check out my paper here.